- PFDS指Purely Functional Data Structure。
- 算是给N年前没能坚持看完Chris Okasaki的论文的自己一个交代。
- 这个是书的PFDS的笔记,不是论文的笔记。
PFDS Note 1
Persistent Leftist Heap
有偏向的二叉堆。
你不直接对堆做destructive update,于是就能够得到历史版本,于是就persistent了。(!)
用有GC+ADT的函数式语言做,一堆要命的细节可以直接省去,简直爽到要飞起来了。(?)
没有任何的政治隐喻。
用Racket写出来则是这样子的:
对于(c),手动将makeT展开即可。
就这样看上去直接写一个C++的也不算太难:
你不直接对堆做destructive update,于是就能够得到历史版本,于是就persistent了。(!)
用有GC+ADT的函数式语言做,一堆要命的细节可以直接省去,简直爽到要飞起来了。(?)
偏向
设有某个rank计算函数R(x),Leftist tree是一种对于任意非叶节点的节点T(left child, elem, right child),有:- R(left child) >= R(right child)
- R(T) = min2(R(left child), R(right child)) + 1
makeT
makeT用来构造保证了左倾的非叶节点。用Standard ML写出来是这样:
(* 假设有:
datatype Heap = E | T of int * ElemType * Heap * Heap
其中ElemType是有total order关系的类型。 *)
fun rank E = 0
| rank (T (r, _, _, _)) = r
fun makeT (x, a, b) =
if rank a >= rank b
then T (rank b + 1, x, a, b)
else T (rank a + 1, x, b, a)
(事实上能不能过编译我是不知道的因为我只学过一点点Standard ML我现在又因为一点个人原因不能立即找个SML实现但是我能看懂所以whatever)用Racket写出来则是这样子的:
#| 假设Heap符合这样的类型:
(define-type (Heap A)
(U '()
(List Exact-Nonnegative-Integer A (Rec Heap A) (Rec Heap A))))
|#
(define (rank t)
(match t
['() 0]
[(list rank1 _ _ _) rank1]))
(define (makeT x a b)
(if (>= (rank a) (rank b))
(list (+ 1 (rank b)) x a b)
(list (+ 1 (rank a)) x b a)))
我们可以看到:
- 为了左倾,rank大的子树被放在了左边。
- 合并后的树的rank是(较小的rank+1)。
merge(还有enque、front和deque)
fun merge (h, E) = x
| merge (E, h) = x
| merge (h1 as T (_, x, a1, b1), h2 as T (_, y, a2, b2)) =
if x <= y
then makeT (x, a1, merge (b1, h2))
else makeT (y, a2, merge (h1, b2))
fun front E = raise Empty
| front (T (_, x, _, _)) = x
fun enque (x, h) = merge (T (1, x, E, E), h)
fun deque E = raise Empty
| deque (T (_, x, a, b)) = merge (a, b)
可以看到最小的元素永远是树的根;左倾由makeT保证。有一点需要注意的是:merge出来的树并不一定是平衡的。不要慌,这是用来搞priority queue的,你又不会在里面find,保证deque最坏O(logn)就够了。考虑这么一种情况:
2
/
3
/
4
/
5
按照merge和deque的定义,每一次deque都是O(1)的,怕个毛线。
Exercise 3.4: Weight-biased lefitst heap
从height-biased改成weight-biased异常简单,改变rank的计算方式即可:
(define (ex3-4-makeT x a b)
(if (>= (rank a) (rank b))
(list (+ 1 (rank a) (rank b)) x a b)
(list (+ 1 (rank a) (rank b)) x b a)))
为什么是(+ 1 (rank a) (rank b))?因为那就是merge出来的树的大小……对于(c),手动将makeT展开即可。
就这样看上去直接写一个C++的也不算太难:
#include<stdio.h>
template<typename T>
class LeftistHeap{
public:
int rank;
T value;
LeftistHeap< T >* left;
LeftistHeap< T >* right;
LeftistHeap< T >(){}
LeftistHeap< T >(int r, T v, LeftistHeap< T >* l, LeftistHeap< T >* rr){
rank = r, value = v, left = l, right = rr;
}
void operator=(LeftistHeap< T >* h){
rank = h->rank, value = h->value, left = h->left, right = h->right;
}
};
template<typename T>
int rank(LeftistHeap< T >* h){ return h?h->rank:0; }
template<typename T>
LeftistHeap< T >* makeT(T value, LeftistHeap< T >* left, LeftistHeap< T >* right){
int rnkA = rank<T>(left), rnkB = rank<T>(right);
LeftistHeap< T >* res;
if(rnkA >= rnkB){
res = new LeftistHeap< T >(rnkB+1, value, left, right);
} else {
res = new LeftistHeap< T >(rnkA+1, value, right, left);
}
return res;
}
template<typename T>
LeftistHeap< T >* merge(LeftistHeap< T >* left, LeftistHeap< T >* right){
if(!left){
return right;
} else if(!right){
return left;
} else {
if(left->value <= right->value){
return makeT<T>(left->value, left->left, merge<T>(left->right, right));
} else {
return makeT<T>(right->value, right->left, merge<T>(left, right->right));
}
}
}
template<typename T>
T front(LeftistHeap< T >* h){
return h->value;
}
template<typename T>
LeftistHeap< T >* enque(T value, LeftistHeap< T >* h){
LeftistHeap< T >* singletonT = new LeftistHeap< T >(1,value,NULL,NULL);
return merge(singletonT, h);
}
template<typename T>
LeftistHeap< T >* deque(LeftistHeap< T >* h){
if(!h) return h;
else {
return merge(h->left, h->right);
}
}
template<typename T>
bool isEmpty(LeftistHeap< T >* h){
if(h)return false; else return true;
}
int main(){
int n;
scanf("%d",&n);
LeftistHeap< int >*heap = NULL;
for(int i=0;i<n;i++){
int A; scanf("%d",&A);
heap = enque< int >(A, heap);
}
printf("-> ");
while(!(isEmpty< int >(heap))){
printf("%d ",front< int >(heap));
heap = deque< int >(heap);
}
putchar('\n');
return 0;
}
/*
5
8 3 4 6 9
-> 3 4 6 8 9
*/
不过内存管理是个难题。可以考虑上Boehm GC。
复杂度
- front时间复杂度O(1)。
- merge时间复杂度O(logn),空间复杂度(通过makeT)O(logn)。
- enque和deque都是某种merge,因此时间/空间复杂度跟merge相同,为O(logn)。
Persistent Binomial Heap
一棵rank 0的Binomial tree仅由一个包含了元素的节点组成。
一棵rank n的Binomial tree由:
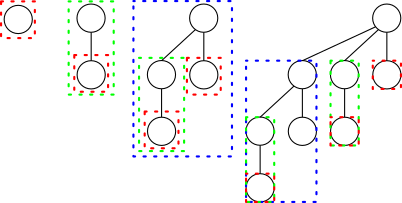
上图分别为rank 0,rank 1,rank 2和rank 3的binomial tree。你们可以一下子看出来rank n的树的第k层有Cnk-1个节点。
于是,我们有link:
enque具体是这样:
顺带一提我们也因此顺带保证了堆里的树永远是按rank从小到大排序的。
对于deleteMin则需要更加仔细的考虑:被delete掉的min一定是堆内某棵binomial树的根,而这棵binomial树去掉根节点之后剩下的子树正好也可以是一个binomial堆,只不过这些子树在原binomial树中排列的顺序正好相反。于是就有:
一棵rank n的Binomial tree由:
- 一个元素(假设为A)。
- 一组(rank n-1, rank n-2, ..., rank 0)根节点的元素都小于等于A(如果是最大堆则为大于等于A)的Binomial tree,按rank n-1,rank n-2,……,rank 0的顺序作为根节点的子树

上图分别为rank 0,rank 1,rank 2和rank 3的binomial tree。你们可以一下子看出来rank n的树的第k层有Cnk-1个节点。
datatype Tree = Node of int * ElemType * Tree list
(* Tree 由 rank 元素 一系列子树 组成 *)
一个Binomial heap由一组按rank从小到大排列的Binomial tree组成。
type Heap = Tree list
或者说,一棵rank n的binomial tree是由两颗rank n-1的binomial tree组成的,其中root较大的树作为root较小的树的最左边的子树(如果是最大堆,则为root较小的树作为子树)。于是,我们有link:
fun link (t1 as Node (r, x1, c1), t2 as Node (_, x2, c2)) =
if x1 < x2
then Node (r + 1, x1, t2 :: c1)
else Node (r + 1, x2, t1 :: c2)
会在别的地方保证只会出现link两个rank相等的树的情况的so don't worry.enque具体是这样:
- 将待enque的元素lift成一棵rank 0的树。
- 假如当前堆中rank最小的树的rank大于0,那么直接将这棵树加进堆里。
- 假如当前堆中rank最小的树的rank等于0,那么结果就等于这两棵树link之后得到的树加进除掉了最小rank的树的堆的结果。
- 我们有20 = 1。
- 假如待加数的least significant bit不在20,那么我们就直接+1。
- 假如待加数的least significant bit在20,那么结果就等于这个lsb跟1相加(link)的结果与除去了这一lsb的待加数相加得到的结果。
顺带一提我们也因此顺带保证了堆里的树永远是按rank从小到大排序的。
fun insTree (t, []) = [t]
| insTree (t, ts as t' :: ts') =
if rank t < rank t'
then t :: ts
else insTree (link (t, t'), ts')
fun insert (x, ts) = insTree (Node (0, x, []), ts)
而merge类似于两个二进制数相加,link操作则类似于加法中的进位:
- 我们找出两个数的least significant bit。
- 假如它们在同一个位置,结果就等于这两个bit的和与去掉这两个bit的两个待加数的和相加得到的和。
1 0 0 0 [1] 0 [1] 0 1 0 0 0 0 0 1 0 0 + 1 0 0 0 [1] 0 <===> + [1] 0 + 1 0 0 0 0 0 + 1 0 0 0 0 0 0 --------------- ------- ------------- --------------- 1 0 0 0 1 0 0 1 0 0 1 0 0 0 0 0 0 1 0 0 0 1 0 0 - 假如不在同一个位置,结果就等于这两个bit中较低位的bit与:
- 这个bit所属的待加数,去掉了这一个bit之后的结果
- 另外一个待加数
1 0 0 0 0 [1] 1 0 0 0 0 0 1 + 1 0 0 0 [1] 0 <===> + 1 0 0 0 1 0 + 1 0 0 0 0 1 0 ----------------- ------------- --------------- 1 0 0 0 0 1 1 1 0 0 0 0 1 0 1 0 0 0 0 1 1
fun merge (ts1, []) = ts1 (* 这里 *)
| merge ([], ts2) = ts2 (* 和这里,都相当于某个数加0 *)
| merge (ts1 as t1 :: ts1', ts2 as t2 :: ts2') =
if rank t1 < t2 then t1 :: merge (ts1', ts2)
else if rank t2 < rank t1 then t2 :: merge (ts1, ts2')
else insTree (link (t1, t2), merge (ts1', ts2'))
现在让我们来考虑findMin(front)和deleteMin(deque)吧。findMin可以额外耗费O(1)的空间达到O(1)的时间复杂度。做法很简单,维护堆中所有binomial树的同时维护一个用于存放当前堆顶元素的currentMin,insert的时候先根据插入元素是否小于currentMin判断是否需要修改currentMin,然后再进行一般的insert。这一多出来的操作是O(1)的,因此insert总体时间复杂度还是O(logn);findMin时直接输出currentMin即可,时间复杂度O(1)。事实上对所有类型的堆都可以这么做。对于deleteMin则需要更加仔细的考虑:被delete掉的min一定是堆内某棵binomial树的根,而这棵binomial树去掉根节点之后剩下的子树正好也可以是一个binomial堆,只不过这些子树在原binomial树中排列的顺序正好相反。于是就有:
fun deleteMin ts =
let val (Node (_, x, ts1), ts2) = removeMinTree ts
in merge (rev ts1, ts2) end
其中的rev就是reverse,而removeMinTree是将堆分割为「根最小的树」和「去掉这棵树后的堆」两个部分的函数:
fun removeMinTree [t] = (t, [])
| removeMinTree (t :: ts) =
let val (t', ts') = removeMinTree ts
in if root t <= root t' then (t, ts) else (t', t :: ts') end
findMin也有O(logn)的做法:
fun findMin h = let val (t', _) = removeMinTree h in root t' end
Red-Black Tree
红黑树是这样的树:
- 每一个非空节点都带上一个颜色(红或者黑);空节点默认为黑节点。
- 红色节点不能有红色的子节点;这同时也是在说,一个红色的节点也不能有一个红色的父节点。
- 从根出发到每一个空节点的路径上所经过的黑色节点数相同。
datatype Color = R | B
datatype Tree = E | T of Color * Tree * ElemType * Tree
不平衡的二叉搜索树在输入已排序时会退化到insert&member O(n)时间复杂度。红黑树对树本身做了一些修改和限制,保证就算这棵树不是完全平衡的,时间复杂度也不会退化得那么严重,还是停留在O(logn)水平。
member跟普通的二叉搜索树的member是一样的:
fun member (x, E) = false
| member (x, T (_, a, y, b)) =
if x < y then member (x, a)
else if x > y then member (x, b)
else true
但是为了保证「红色的节点没有红色的子节点」,insert稍有不同:
fun insert (x, s) =
let fun ins E = T (R, E, x, E)
| ins (s as T (color, a, y, b)) =
if x < y then balance (color, ins a, y, b)
else if x > y then balance (color, a, y, ins b)
else s
val T (_, a, y, b) = ins s
in T (B, a, y, b) end
有几点需要注意的是:
- ins里建立新的节点时颜色设为红色是为了保证「根节点到所有的空节点的路径中所经黑色节点个数相等」。
- 而这种做法可能导致这棵树不遵循「红色的节点不能有红色的子节点」这一限制,所以我们用balance来改变这一点(注意这里没有直接用value constructor T;之前在leftist heap中也用了一个类似的函数makeT来顺带保证一些必要的性质。),这样我们就能保证每一层都不会出现这种情况了。
- 根节点颜色设为黑色,是为了在不违反关于黑色节点个数的限制的同时保证红色节点没有红色子节点。(因为是整棵树的根节点,所以它会出现在所有到空节点的路径上,所以不管是红色还是黑色都合法。)
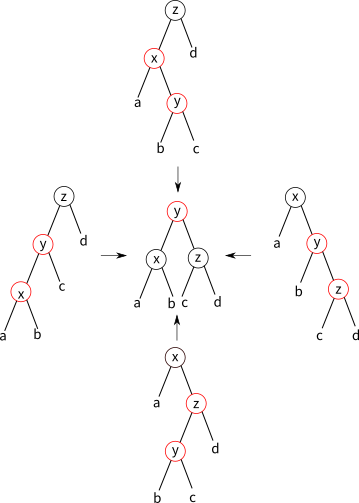
fun balance (B, T(R, T(R,a,x,b), y, c), z, d) = T (R, T(B,a,x,b), y, T(B,c,z,d))
| balance (B, T(R, a, x, T(R,b,y,c)), z, d) = T (R, T(B,a,x,b), y, T(B,c,z,d))
| balance (B, a, x, T(R, T(R,b,y,c), z, d)) = T (R, T(B,a,x,b), y, T(B,c,z,d))
| balance (B, a, x, T(R, b, y, T(R,c,z,d))) = T (R, T(B,a,x,b), y, T(B,c,z,d))
| balance body = T body
进行了这样的操作: